Log wind profile
The Log wind profile is a semi-empirical relationship used to describe the vertical distribution of horizontal wind speeds above the ground within the atmospheric surface layer. The relationship is well described in the planetary boundary layer literature [1].
The logarithmic profile of wind speeds is generally limited to the lowest 100 meters (325') of the atmosphere (i.e., the surface layer of the atmospheric boundary layer). The rest of the atmosphere is composed of the remaining part of the planetary boundary layer (up to around 1000m) and the troposphere or free atmosphere. In the free atmosphere, geostrophic wind relationships should be used. The equation to estimate the wind speed ( ) at height
) at height 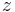 (meters) above the ground is:
(meters) above the ground is:
![u_z = \frac{u_*}{\kappa} \left[\ln \left(\frac{z-d}{z_0} \right) %2B \psi(z,z_0,L)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/1c2ccd5ff80f41ab526ea9e138cf39fd.png)
where 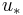 is the friction (or shear) velocity (m s-1),
is the friction (or shear) velocity (m s-1),  is von Karman's constant (~0.41),
is von Karman's constant (~0.41),  is the zero plane displacement,
is the zero plane displacement, 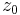 is the surface roughness (in meters), and
is the surface roughness (in meters), and  is a stability term where
is a stability term where  is the Monin-Obukhov stability parameter. Under neutral stability conditions,
is the Monin-Obukhov stability parameter. Under neutral stability conditions, 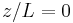 and
and  drops out.
drops out.
Zero-plane displacement ( ) is the height in meters above the ground at which zero wind speed is achieved as a result of flow obstacles such as trees or buildings. It is generally approximated as 2/3 of the average height of the obstacles. For example, if estimating winds over a forest canopy of height h = 30 m, the zero-plane displacement would be d = 20 m.
) is the height in meters above the ground at which zero wind speed is achieved as a result of flow obstacles such as trees or buildings. It is generally approximated as 2/3 of the average height of the obstacles. For example, if estimating winds over a forest canopy of height h = 30 m, the zero-plane displacement would be d = 20 m.
Roughness length (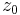 ) is a corrective measure to account for the effect of the roughness of a surface on wind flow, and is between 1/10 and 1/30 of the average height of the roughness elements on the ground. Over smooth, open water, expect a value around 0.0002 m, while over flat, open grassland
) is a corrective measure to account for the effect of the roughness of a surface on wind flow, and is between 1/10 and 1/30 of the average height of the roughness elements on the ground. Over smooth, open water, expect a value around 0.0002 m, while over flat, open grassland 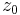 ≈ 0.03 m, cropland ≈ 0.1-0.25 m, and brush or forest ≈ 0.5-1.0 m (values above 1 m are rare and indicate excessively rough terrain).
≈ 0.03 m, cropland ≈ 0.1-0.25 m, and brush or forest ≈ 0.5-1.0 m (values above 1 m are rare and indicate excessively rough terrain).
The log wind profile is generally considered to be a more reliable estimator than the Wind profile power law, which is commonly used when neutral conditions are assumed and roughness information is not available.
Applications
Log wind profiles are generated and used in many atmospheric pollution dispersion models.[2]
See also
References
- ^ Oke, T.R. (1987). Boundary Layer Climates. Methuen.
- ^ Beychok, Milton R. (2005). Fundamentals Of Stack Gas Dispersion (4th Edition ed.). author-published. ISBN 0-9644588-0-2.